Simhash 小记

Simhash 最早是Google 用来对海量的数据文本进行去重的算法，算法的原理很简单，但很实用。

1、simhash的第一步是对每个要去重的文本集合进行Finger Print 计算，计算方法如下图：

算法过程大概如下：

1. 将Doc进行关键词抽取(其中包括分词和计算权重)，抽取出n个(关键词，权重)对， 即图中的(feature, weight)们。 记为 feature_weight_pairs = [fw1, fw2 … fwn]，其中 fwn = (feature_n,weight_n`)。
2. hash_weight_pairs = [ (hash(feature), weight) for feature, weight infeature_weight_pairs ] 生成图中的(hash,weight)们, 此时假设hash生成的位数bits_count = 6（如图）;
3. 然后对 hash_weight_pairs 进行位的纵向累加，如果该位是1，则+weight,如果是0，则-weight，最后生成bits_count个数字，如图所示是[13, 108, -22, -5, -32, 55], 这里产生的值和hash函数所用的算法相关。
4. [13,108,-22,-5,-32,55] -> 110001这个就很简单啦，正1负0。

simhash和普通hash最大的不同在于传统的hash函数虽然也可以用于映射来比较文本的重复，但是对于可能差距只有一个字节的文档也会映射成两个完全不同的哈希结果，而simhash对相似的文本的哈希映射结果也相似。Google的论文中取了f=64，即将整个网页的加权特征集合映射到一个64-bit的fingerprint上。

2、

『simhash值的海明距离计算』

二进制串A 和 二进制串B 的海明距离 就是 A xor B 后二进制中1的个数。

举例如下：

A = 100111;
B = 101010;
hamming_distance(A, B) = count_1(A xor B) = count_1(001101) = 3;

当我们算出所有doc的simhash值之后，需要计算doc A和doc B之间是否相似的条件是：

A和B的海明距离是否小于等于n，这个n值根据经验一般取值为3,

simhash本质上是局部敏感性的hash，和md5之类的不一样。 正因为它的局部敏感性，所以我们可以使用海明距离来衡量simhash值的相似度。

『高效计算二进制序列中1的个数』

/* src/Simhasher.hpp */
bool isEqual(uint64_t lhs, uint64_t rhs, unsigned short n = 3)
{
    unsigned short cnt = 0;
    lhs ^= rhs;
    while(lhs && cnt <= n)
    {
        lhs &= lhs - 1;
        cnt++;
    }
    if(cnt <= n)
    {
        return true;
    }
    return false;
}

由上式这个函数来计算的话，时间复杂度是 O(n); 这里的n默认取值为3。由此可见还是蛮高效的。

simhash 实现的工程项目

• C++ 版本 simhash
• Golang 版本 gosimhash

主要是针对中文文档，也就是此项目进行simhash之前同时还进行了分词和关键词的抽取。

 

应用

• 每篇文档得到SimHash签名值后，接着计算两个签名的海明距离即可。根据经验值，对64位的 SimHash值，海明距离在3以内的可认为相似度比较高。
  • 海明距离的求法：异或时，只有在两个比较的位不同时其结果是1 ，否则结果为0，两个二进制“异或”后得到1的个数即为海明距离的大小。

举个例子，上面我们计算到的“CSDN博客”的simhash签名值为“1 0 1 0 1 1”，假定我们计算出另外一个短语的签名值为“1 0 1 0 0 0”，那么根据异或规则，我们可以计算出这两个签名的海明距离为2，从而判定这两个短语的相似度是比较高的。

换言之，现在问题转换为：对于64位的SimHash值，我们只要找到海明距离在3以内的所有签名，即可找出所有相似的短语。

但关键是，如何将其扩展到海量数据呢？譬如如何在海量的样本库中查询与其海明距离在3以内的记录呢？

• 一种方案是查找待查询文本的64位simhash code的所有3位以内变化的组合
  • 大约需要四万多次的查询。
• 另一种方案是预生成库中所有样本simhash code的3位变化以内的组合
  • 大约需要占据4万多倍的原始空间。

这两种方案，要么时间复杂度高，要么空间复杂度复杂，能否有一种方案可以达到时空复杂度的绝佳平衡呢？答案是肯定的：

• 我们可以把 64 位的二进制simhash签名均分成4块，每块16位。根据鸽巢原理（也称抽屉原理），如果两个签名的海明距离在 3 以内，它们必有一块完全相同。如下图所示：
• 然后把分成的4 块中的每一个块分别作为前16位来进行查找，建倒排索引。

具体如下图所示：

如此，如果样本库中存有2^34（差不多10亿）的simhash签名，则每个table返回2^(34-16)=262144个候选结果，大大减少了海明距离的计算成本。

• 假设数据是均匀分布，16位的数据，产生的像限为2^16个，则平均每个像限分布的文档数则为2^34/2^16 = 2^(34-16)) ，四个块返回的总结果数为 4* 262144 （大概 100 万）。
  • 这样，原本需要比较10亿次，经过索引后，大概只需要处理100万次。

 

【References】

http://leoncom.org/?p=650607

http://taop.marchtea.com/06.03.html

Understanding EM Algorithms

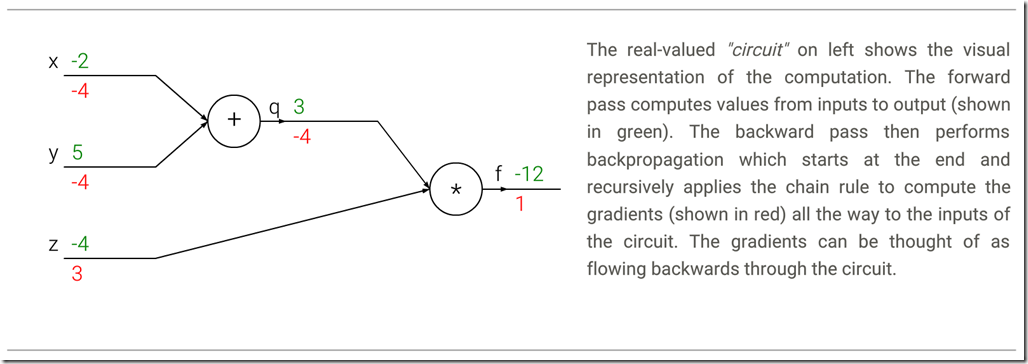
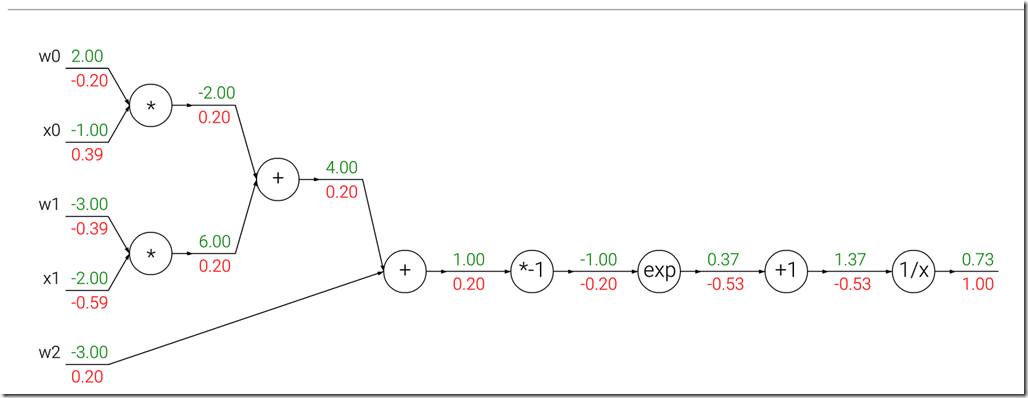
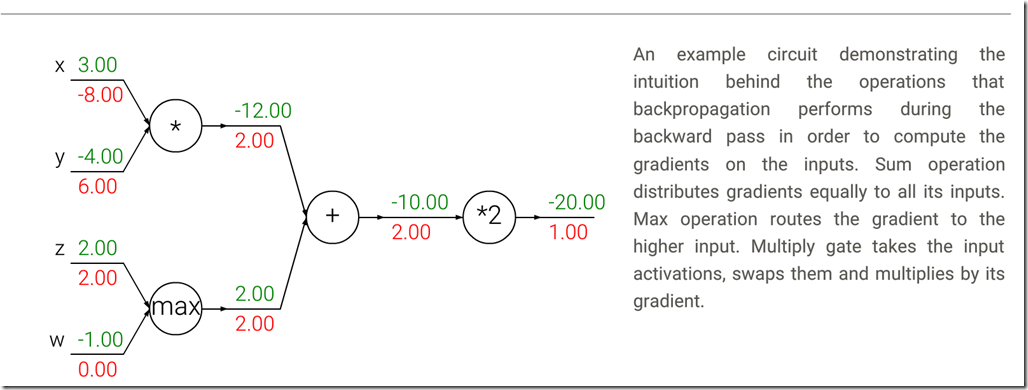
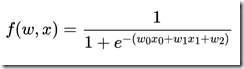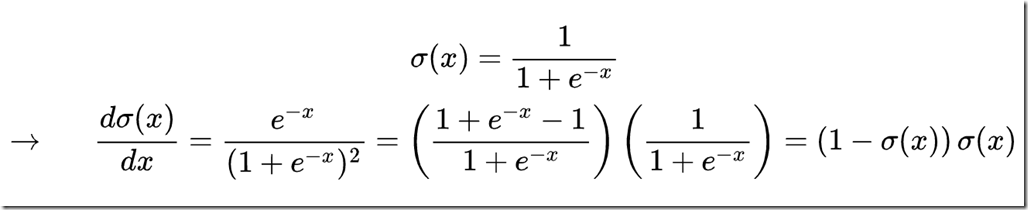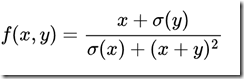[开篇说明]：这篇文章转自zouxy09的CSDN博客， 之所以转发过来是因为觉得文中对于EM的讲解逻辑和对于EM的引子引入的恰到好处，相信很多人都会很容易就理解。

用“鸡生蛋，蛋生鸡”的问题来引入EM简直再好不过；由此引出的“索性先初始化一坨参数值”，再“不断迭代收敛”从而得到最终param 的阐述也很到位。

总之，简单明了，很适合初学者一看。

<正文>

       机器学习十大算法之一：EM算法。能评得上十大之一，让人听起来觉得挺NB的。什么是NB啊，我们一般说某个人很NB，是因为他能解决一些别人解决不了的问题。神为什么是神，因为神能做很多人做不了的事。那么EM算法能解决什么问题呢？或者说EM算法是因为什么而来到这个世界上，还吸引了那么多世人的目光。

我希望自己能通俗地把它理解或者说明白，但是，EM这个问题感觉真的不太好用通俗的语言去说明白，因为它很简单，又很复杂。简单在于它的思想，简单在于其仅包含了两个步骤就能完成强大的功能，复杂在于它的数学推理涉及到比较繁杂的概率公式等。如果只讲简单的，就丢失了EM算法的精髓，如果只讲数学推理，又过于枯燥和生涩，但另一方面，想把两者结合起来也不是件容易的事。所以，我也没法期待我能把它讲得怎样。希望各位不吝指导。

 

一、最大似然

扯了太多，得入正题了。假设我们遇到的是下面这样的问题：

假设我们需要调查我们学校的男生和女生的身高分布。你怎么做啊？你说那么多人不可能一个一个去问吧，肯定是抽样了。假设你在校园里随便地活捉了100个男生和100个女生。他们共200个人（也就是200个身高的样本数据，为了方便表示，下面，我说“人”的意思就是对应的身高）都在教室里面了。那下一步怎么办啊？你开始喊：“男的左边，女的右边，其他的站中间！”。然后你就先统计抽样得到的100个男生的身高。假设他们的身高是服从高斯分布的。但是这个分布的均值u和方差∂²我们不知道，这两个参数就是我们要估计的。记作θ=[u, ∂]^T。

用数学的语言来说就是：在学校那么多男生（身高）中，我们独立地按照概率密度p(x|θ)抽取100了个（身高），组成样本集X，我们想通过样本集X来估计出未知参数θ。这里概率密度p(x|θ)我们知道了是高斯分布N(u,∂)的形式，其中的未知参数是θ=[u, ∂]^T。抽到的样本集是X={x₁,x₂,…,x_N}，其中x_i表示抽到的第i个人的身高，这里N就是100，表示抽到的样本个数。

由于每个样本都是独立地从p(x|θ)中抽取的，换句话说这100个男生中的任何一个，都是我随便捉的，从我的角度来看这些男生之间是没有关系的。那么，我从学校那么多男生中为什么就恰好抽到了这100个人呢？抽到这100个人的概率是多少呢？因为这些男生（的身高）是服从同一个高斯分布p(x|θ)的。那么我抽到男生A（的身高）的概率是p(x_A|θ)，抽到男生B的概率是p(x_B|θ)，那因为他们是独立的，所以很明显，我同时抽到男生A和男生B的概率是p(x_A|θ)* p(x_B|θ)，同理，我同时抽到这100个男生的概率就是他们各自概率的乘积了。用数学家的口吻说就是从分布是p(x|θ)的总体样本中抽取到这100个样本的概率，也就是样本集X中各个样本的联合概率，用下式表示：

这个概率反映了，在概率密度函数的参数是θ时，得到X这组样本的概率。因为这里X是已知的，也就是说我抽取到的这100个人的身高可以测出来，也就是已知的了。而θ是未知了，则上面这个公式只有θ是未知数，所以它是θ的函数。这个函数放映的是在不同的参数θ取值下，取得当前这个样本集的可能性，因此称为参数θ相对于样本集X的似然函数（likehood function）。记为L(θ)。

这里出现了一个概念，似然函数。还记得我们的目标吗？我们需要在已经抽到这一组样本X的条件下，估计参数θ的值。怎么估计呢？似然函数有啥用呢？那咱们先来了解下似然的概念。

直接举个例子：

某位同学与一位猎人一起外出打猎，一只野兔从前方窜过。只听一声枪响，野兔应声到下，如果要你推测，这一发命中的子弹是谁打的？你就会想，只发一枪便打中，由于猎人命中的概率一般大于这位同学命中的概率，看来这一枪是猎人射中的。

这个例子所作的推断就体现了极大似然法的基本思想。

再例如：下课了，一群男女同学分别去厕所了。然后，你闲着无聊，想知道课间是男生上厕所的人多还是女生上厕所的人比较多，然后你就跑去蹲在男厕和女厕的门口。蹲了五分钟，突然一个美女走出来，你狂喜，跑过来告诉我，课间女生上厕所的人比较多，你要不相信你可以进去数数。呵呵，我才没那么蠢跑进去数呢，到时还不得上头条。我问你是怎么知道的。你说：“5分钟了，出来的是女生，女生啊，那么女生出来的概率肯定是最大的了，或者说比男生要大，那么女厕所的人肯定比男厕所的人多”。看到了没，你已经运用最大似然估计了。你通过观察到女生先出来，那么什么情况下，女生会先出来呢？肯定是女生出来的概率最大的时候了，那什么时候女生出来的概率最大啊，那肯定是女厕所比男厕所多人的时候了，这个就是你估计到的参数了。

从上面这两个例子，你得到了什么结论？

回到男生身高那个例子。在学校那么男生中，我一抽就抽到这100个男生（表示身高），而不是其他人，那是不是表示在整个学校中，这100个人（的身高）出现的概率最大啊。那么这个概率怎么表示？哦，就是上面那个似然函数L(θ)。所以，我们就只需要找到一个参数θ，其对应的似然函数L(θ)最大，也就是说抽到这100个男生（的身高）概率最大。这个叫做θ的最大似然估计量，记为：

有时，可以看到L(θ)是连乘的，所以为了便于分析，还可以定义对数似然函数，将其变成连加的：

好了，现在我们知道了，要求θ，只需要使θ的似然函数L(θ)极大化，然后极大值对应的θ就是我们的估计。这里就回到了求最值的问题了。怎么求一个函数的最值？当然是求导，然后让导数为0，那么解这个方程得到的θ就是了（当然，前提是函数L(θ)连续可微）。那如果θ是包含多个参数的向量那怎么处理啊？当然是求L(θ)对所有参数的偏导数，也就是梯度了，那么n个未知的参数，就有n个方程，方程组的解就是似然函数的极值点了，当然就得到这n个参数了。

最大似然估计你可以把它看作是一个反推。多数情况下我们是根据已知条件来推算结果，而最大似然估计是已经知道了结果，然后寻求使该结果出现的可能性最大的条件，以此作为估计值。比如，如果其他条件一定的话，抽烟者发生肺癌的危险时不抽烟者的5倍，那么如果现在我已经知道有个人是肺癌，我想问你这个人抽烟还是不抽烟。你怎么判断？你可能对这个人一无所知，你所知道的只有一件事，那就是抽烟更容易发生肺癌，那么你会猜测这个人不抽烟吗？我相信你更有可能会说，这个人抽烟。为什么？这就是“最大可能”，我只能说他“最有可能”是抽烟的，“他是抽烟的”这一估计值才是“最有可能”得到“肺癌”这样的结果。这就是最大似然估计。

好了，极大似然估计就讲到这，总结一下：

极大似然估计，只是一种概率论在统计学的应用，它是参数估计的方法之一。说的是已知某个随机样本满足某种概率分布，但是其中具体的参数不清楚，参数估计就是通过若干次试验，观察其结果，利用结果推出参数的大概值。最大似然估计是建立在这样的思想上：已知某个参数能使这个样本出现的概率最大，我们当然不会再去选择其他小概率的样本，所以干脆就把这个参数作为估计的真实值。

求最大似然函数估计值的一般步骤：

（1）写出似然函数；

（2）对似然函数取对数，并整理；

（3）求导数，令导数为0，得到似然方程；

（4）解似然方程，得到的参数即为所求；

 

二、EM算法

好了，重新回到上面那个身高分布估计的问题。现在，通过抽取得到的那100个男生的身高和已知的其身高服从高斯分布，我们通过最大化其似然函数，就可以得到了对应高斯分布的参数θ=[u, ∂]^T了。那么，对于我们学校的女生的身高分布也可以用同样的方法得到了。

再回到例子本身，如果没有“男的左边，女的右边，其他的站中间！”这个步骤，或者说我抽到这200个人中，某些男生和某些女生一见钟情，已经好上了，纠缠起来了。咱们也不想那么残忍，硬把他们拉扯开。那现在这200个人已经混到一起了，这时候，你从这200个人（的身高）里面随便给我指一个人（的身高），我都无法确定这个人（的身高）是男生（的身高）还是女生（的身高）。也就是说你不知道抽取的那200个人里面的每一个人到底是从男生的那个身高分布里面抽取的，还是女生的那个身高分布抽取的。用数学的语言就是，抽取得到的每个样本都不知道是从哪个分布抽取的。

这个时候，对于每一个样本或者你抽取到的人，就有两个东西需要猜测或者估计的了，一是这个人是男的还是女的？二是男生和女生对应的身高的高斯分布的参数是多少？

只有当我们知道了哪些人属于同一个高斯分布的时候，我们才能够对这个分布的参数作出靠谱的预测，例如刚开始的最大似然所说的，但现在两种高斯分布的人混在一块了，我们又不知道哪些人属于第一个高斯分布，哪些属于第二个，所以就没法估计这两个分布的参数。反过来，只有当我们对这两个分布的参数作出了准确的估计的时候，才能知道到底哪些人属于第一个分布，那些人属于第二个分布。

这就成了一个先有鸡还是先有蛋的问题了。鸡说，没有我，谁把你生出来的啊。蛋不服，说，没有我，你从哪蹦出来啊。（呵呵，这是一个哲学问题。当然了，后来科学家说先有蛋，因为鸡蛋是鸟蛋进化的）。为了解决这个你依赖我，我依赖你的循环依赖问题，总得有一方要先打破僵局，说，不管了，我先随便整一个值出来，看你怎么变，然后我再根据你的变化调整我的变化，然后如此迭代着不断互相推导，最终就会收敛到一个解。这就是EM算法的基本思想了。

不知道大家能否理解其中的思想，我再来啰嗦一下。其实这个思想无处在不啊。

例如，小时候，老妈给一大袋糖果给你，叫你和你姐姐等分，然后你懒得去点糖果的个数，所以你也就不知道每个人到底该分多少个。咱们一般怎么做呢？先把一袋糖果目测的分为两袋，然后把两袋糖果拿在左右手，看哪个重，如果右手重，那很明显右手这代糖果多了，然后你再在右手这袋糖果中抓一把放到左手这袋，然后再感受下哪个重，然后再从重的那袋抓一小把放进轻的那一袋，继续下去，直到你感觉两袋糖果差不多相等了为止。呵呵，然后为了体现公平，你还让你姐姐先选了。

EM算法就是这样，假设我们想估计知道A和B两个参数，在开始状态下二者都是未知的，但如果知道了A的信息就可以得到B的信息，反过来知道了B也就得到了A。可以考虑首先赋予A某种初值，以此得到B的估计值，然后从B的当前值出发，重新估计A的取值，这个过程一直持续到收敛为止。

EM的意思是“Expectation Maximization”，在我们上面这个问题里面，（例子）我们是先随便猜一下男生（身高）的正态分布的参数：如均值和方差是多少。例如男生的均值是1米7，方差是0.1米（当然了，刚开始肯定没那么准），然后计算出每个人更可能属于第一个还是第二个正态分布中的（例如，这个人的身高是1米8，那很明显，他最大可能属于男生的那个分布），这个是属于Expectation一步。有了每个人的归属，或者说我们已经大概地按上面的方法将这200个人分为男生和女生两部分，我们就可以根据之前说的最大似然那样，通过这些被大概分为男生的n个人来重新估计第一个分布的参数，女生的那个分布同样方法重新估计。这个是Maximization。然后，当我们更新了这两个分布的时候，每一个属于这两个分布的概率又变了，那么我们就再需要调整E步……如此往复，直到参数基本不再发生变化为止。

这里把每个人（样本）的完整描述看做是三元组y_i={x_i,z_i1,z_i2}，其中，x_i是第i个样本的观测值，也就是对应的这个人的身高，是可以观测到的值。z_i1和z_i2表示男生和女生这两个高斯分布中哪个被用来产生值x_i，就是说这两个值标记这个人到底是男生还是女生（的身高分布产生的）。这两个值我们是不知道的，是隐含变量。确切的说，z_ij在x_i由第j个高斯分布产生时值为1，否则为0。例如一个样本的观测值为1.8，然后他来自男生的那个高斯分布，那么我们可以将这个样本表示为{1.8, 1, 0}。如果z_i1和z_i2的值已知，也就是说每个人我已经标记为男生或者女生了，那么我们就可以利用上面说的最大似然算法来估计他们各自高斯分布的参数。但是它们未知，因此我们只能用EM算法。

咱们现在不是因为那个恶心的隐含变量（抽取得到的每个样本都不知道是从哪个分布抽取的）使得本来简单的可以求解的问题变复杂了，求解不了吗。那怎么办呢？人类解决问题的思路都是想能否把复杂的问题简单化。好，那么现在把这个复杂的问题逆回来，我假设已经知道这个隐含变量了，哎，那么求解那个分布的参数是不是很容易了，直接按上面说的最大似然估计就好了。那你就问我了，这个隐含变量是未知的，你怎么就来一个假设说已知呢？你这种假设是没有根据的。呵呵，我知道，所以我们可以先给这个给分布弄一个初始值，然后求这个隐含变量的期望，当成是这个隐含变量的已知值，那么现在就可以用最大似然求解那个分布的参数了吧，那假设这个参数比之前的那个随机的参数要好，它更能表达真实的分布，那么我们再通过这个参数确定的分布去求这个隐含变量的期望，然后再最大化，得到另一个更优的参数，……迭代，就能得到一个皆大欢喜的结果了。

这时候你就不服了，说你老迭代迭代的，你咋知道新的参数的估计就比原来的好啊？为什么这种方法行得通呢？有没有失效的时候呢？什么时候失效呢？用到这个方法需要注意什么问题呢？呵呵，一下子抛出那么多问题，搞得我适应不过来了，不过这证明了你有很好的搞研究的潜质啊。呵呵，其实这些问题就是数学家需要解决的问题。在数学上是可以稳当的证明的或者得出结论的。那咱们用数学来把上面的问题重新描述下。（在这里可以知道，不管多么复杂或者简单的物理世界的思想，都需要通过数学工具进行建模抽象才得以使用并发挥其强大的作用，而且，这里面蕴含的数学往往能带给你更多想象不到的东西，这就是数学的精妙所在啊）

 

三、EM算法推导

假设我们有一个样本集{x⁽¹⁾,…,x^(m)}，包含m个独立的样本。但每个样本i对应的类别z⁽ⁱ⁾是未知的（相当于聚类），也即隐含变量。故我们需要估计概率模型p(x,z)的参数θ，但是由于里面包含隐含变量z，所以很难用最大似然求解，但如果z知道了，那我们就很容易求解了。

对于参数估计，我们本质上还是想获得一个使似然函数最大化的那个参数θ，现在与最大似然不同的只是似然函数式中多了一个未知的变量z，见下式（1）。也就是说我们的目标是找到适合的θ和z让L(θ)最大。那我们也许会想，你就是多了一个未知的变量而已啊，我也可以分别对未知的θ和z分别求偏导，再令其等于0，求解出来不也一样吗？

本质上我们是需要最大化（1）式（对（1）式，我们回忆下联合概率密度下某个变量的边缘概率密度函数的求解，注意这里z也是随机变量。对每一个样本i的所有可能类别z求等式右边的联合概率密度函数和，也就得到等式左边为随机变量x的边缘概率密度），也就是似然函数，但是可以看到里面有“和的对数”，求导后形式会非常复杂（自己可以想象下log(f₁(x)+ f₂(x)+ f₃(x)+…)复合函数的求导），所以很难求解得到未知参数z和θ。那OK，我们可否对（1）式做一些改变呢？我们看（2）式，（2）式只是分子分母同乘以一个相等的函数，还是有“和的对数”啊，还是求解不了，那为什么要这么做呢？咱们先不管，看（3）式，发现（3）式变成了“对数的和”，那这样求导就容易了。我们注意点，还发现等号变成了不等号，为什么能这么变呢？这就是Jensen不等式的大显神威的地方。

Jensen不等式：

设f是定义域为实数的函数，如果对于所有的实数x。如果对于所有的实数x，f(x)的二次导数大于等于0，那么f是凸函数。当x是向量时，如果其hessian矩阵H是半正定的，那么f是凸函数。如果只大于0，不等于0，那么称f是严格凸函数。

Jensen不等式表述如下：

如果f是凸函数，X是随机变量，那么：E[f(X)]>=f(E[X])

特别地，如果f是严格凸函数，当且仅当X是常量时，上式取等号。

如果用图表示会很清晰：

图中，实线f是凸函数，X是随机变量，有0.5的概率是a，有0.5的概率是b。（就像掷硬币一样）。X的期望值就是a和b的中值了，图中可以看到E[f(X)]>=f(E[X])成立。

当f是（严格）凹函数当且仅当-f是（严格）凸函数。

Jensen不等式应用于凹函数时，不等号方向反向。

 

回到公式（2），因为f(x)=log x为凹函数（其二次导数为-1/x²<0）。

（2）式中的期望，（考虑到E(X)=∑x*p(x)，f(X)是X的函数，则E(f(X))=∑f(x)*p(x)），又，所以就可以得到公式（3）的不等式了（若不明白，请拿起笔，呵呵）：

OK，到这里，现在式（3）就容易地求导了，但是式（2）和式（3）是不等号啊，式（2）的最大值不是式（3）的最大值啊，而我们想得到式（2）的最大值，那怎么办呢？

现在我们就需要一点想象力了，上面的式（2）和式（3）不等式可以写成：似然函数L(θ)>=J(z,Q)，那么我们可以通过不断的最大化这个下界J，来使得L(θ)不断提高，最终达到它的最大值。

见上图，我们固定θ，调整Q(z)使下界J(z,Q)上升至与L(θ)在此点θ处相等（绿色曲线到蓝色曲线），然后固定Q(z)，调整θ使下界J(z,Q)达到最大值（θ^t到θ^t+1），然后再固定θ，调整Q(z)……直到收敛到似然函数L(θ)的最大值处的θ*。这里有两个问题：什么时候下界J(z,Q)与L(θ)在此点θ处相等？为什么一定会收敛？

首先第一个问题，在Jensen不等式中说到，当自变量X是常数的时候，等式成立。而在这里，即：

再推导下，由于（因为Q是随机变量z⁽ⁱ⁾的概率密度函数），则可以得到：分子的和等于c（分子分母都对所有z⁽ⁱ⁾求和：多个等式分子分母相加不变，这个认为每个样例的两个概率比值都是c），则：

至此，我们推出了在固定参数θ后，使下界拉升的Q(z)的计算公式就是后验概率，解决了Q(z)如何选择的问题。这一步就是E步，建立L(θ)的下界。接下来的M步，就是在给定Q(z)后，调整θ，去极大化L(θ)的下界J（在固定Q(z)后，下界还可以调整的更大）。那么一般的EM算法的步骤如下：

EM算法（Expectation-maximization）：

期望最大算法是一种从不完全数据或有数据丢失的数据集（存在隐含变量）中求解概率模型参数的最大似然估计方法。

EM的算法流程：

初始化分布参数θ；

重复以下步骤直到收敛：

        E步骤：根据参数初始值或上一次迭代的模型参数来计算出隐性变量的后验概率，其实就是隐性变量的期望。作为隐藏变量的现估计值：

       

        M步骤：将似然函数最大化以获得新的参数值：

这个不断的迭代，就可以得到使似然函数L(θ)最大化的参数θ了。那就得回答刚才的第二个问题了，它会收敛吗？

感性的说，因为下界不断提高，所以极大似然估计单调增加，那么最终我们会到达最大似然估计的最大值。理性分析的话，就会得到下面的东西：

具体如何证明的，看推导过程参考：Andrew Ng《The EM algorithm》

http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006936.html

 

四、EM算法另一种理解

坐标上升法（Coordinate ascent）：

图中的直线式迭代优化的路径，可以看到每一步都会向最优值前进一步，而且前进路线是平行于坐标轴的，因为每一步只优化一个变量。

这犹如在x-y坐标系中找一个曲线的极值，然而曲线函数不能直接求导，因此什么梯度下降方法就不适用了。但固定一个变量后，另外一个可以通过求导得到，因此可以使用坐标上升法，一次固定一个变量，对另外的求极值，最后逐步逼近极值。对应到EM上，E步：固定θ，优化Q；M步：固定Q，优化θ；交替将极值推向最大。

 

五、EM的应用

EM算法有很多的应用，最广泛的就是GMM混合高斯模型、聚类、HMM等等。具体可以参考JerryLead的cnblog中的Machine Learning专栏：

（EM算法）The EM Algorithm

混合高斯模型（Mixtures of Gaussians）和EM算法

K-means聚类算法

 

没有鸡和蛋的先后之争，因为他们都知道“没有你就没有我”。从此他们一起过上了幸福美好的生活。

How to set Architecture of Neural Networks?

【OUTLINE】:

• Neural Networks是对人的神经传递系统的模拟；需要一个activation函数f，通常选sigmoid函数；
• Neural Networks 是一个比较coarse的系统，说它粗糙是因为跟真正的生物神经机能相比，它只能说弱爆了。
• 神经网络中的每一个神经元，即示意图中的每一个圆圈，都可以被看做是一个线性分类器；可以引入诸如Binary Softmax Classifer、Binary SVM classifer、Regularization Interpretation等分类器。
• 通常使用的activation 函数包括：sigmoid, tanh, ReLU, Leaky ReLU, Maxout等；其中sigmoid 是最不推荐使用的，缺点太多；ReLU和Maxout可以一试。
• Neural Networks的架构：它就是一个图，单向无循环图。如何确定一个神经网络是几层的，最后一层通常是一个分数，如何设置一个Neural Networks的大小即复杂度，它的复杂度取决于神经元neuro的个数和整个神经网络的层数。越复杂，则需要学习的parameter数越多，系统也就越复杂。
• Feed-forward Computation：跟上一章提到的forward pass方法类似，只是要注意关于Matrix的计算；
• Representational Power：每一个Neural Networks都定义了相应的函数簇，如何评价一个函数族的表达能力？事实证明，Neural Networks可以表述模拟任何一个连续函数来构建模型。一个2层的神经网络和一个20层的神经网络相比其模拟能力基本相同，现实中，3层的网络往往比2层的效果要好，但是4,5,6层以上对效果的改进就没有那么显著了。
• Setting Number of Layers and their sizes：虽然一个2层的神经网络和一个20层的神经网络相比其模拟能力基本相同，但大量经验表明，深层的系统的确比浅层的效果要好得多。对同一个问题，深层容易陷入overfitting，但是不表示越浅层越好，解决overfitting的方法有很多，如L2，dropout等，所以尽量深层吧。

首先给出一个比拟图，因为神经网络的原理是从人的神经传递结构中想象出来的一种模拟神经传递过程的，所以对于理解Neureal Networks的传递方式的理解可以参考下图：

 

正如上篇文章《How Backpropagation Computes》里提到的计算forward pass和backward pass的计算过程一样，给定初始权重w的值和样本数据x，我们可以很轻松地计算forward-Porpagation在各个阶段的值：（这里的激活函数activiation仍然是sigmoid 函数）

由于Neural Networks 是对人类神经系统的一个简单的模拟，我们不难理解，目前的Neural NetWorks 只不过是神经网络的一个非常粗糙的理论，远远不如真正的生物神经网络发达。

【每一层到下一层的一个节点的映射，可以看做一个linear classifer】

参考下图。事实上，Neural Networks的每一竖层上的节点到下一层的节点的映射过程被理解成了一个linear classifer，如下图第一层到第二层上的每一个节点都是通过一个sigmoid函数的activation过程获取到的，第二层到最终层的过程也是如此。

而可以用作这样的linear classifer的方法有这样一些可供选择：Binary Softmax classifer, Binary SVM classifer, Regularization Interpretation等。

【目前一般会遇到的activation 函数】

1、sigmoid

sigmoid被钟爱的原因是它以real-value为输入，并且具有很好的类别区分性，由于它的取值范围在0-1之间，所以对于defend<0.5的就是negative类，大于0.5的就是positive类。它在很长一段时间被业界频繁使用，但今年貌似已经开始淡出这个范围。

sigmoid有两个缺点：

1）sigmoid的activation值接近0或者1的时候，容易对梯度计算造成影响。见上图，activation值在接近0或者1的时候，曲线的梯度非常小且接近于0，这就会导致在计算backPropagation的时候出现问题，因为存在乘以梯度的过程。

另外，在对sigmoid的参数进行初始化的时候需要注意，如果参数值太大，可能会导致产生上述情况，以致该networks 无法得到训练。所以，尽可能选择比较小的随机参数。

2）由sigmoid的曲线可以看出，它的值不是以0为中心的，而是以0.5为中心，于是sigmoid的函数值只能为正的，这就会导致在backpropagation过程中对参数w进行梯度求解的时候，所有的参数w的梯度都是negative或者都是positive的，至于究竟会是哪个这取决于整个神经网络路线图最后的1,2层梯度值。

虽然这也是个缺点，但是相对于第1）个，这个的影响没有那么明显。

2、tanh

这个比sigmoid要好一些，虽然同样存在在两边的极端情况下偏导数为0的情形，但它却是以0为中心的。

3、除了以上两个，还有ReLU、leaky ReLU、MaxOut等方法，其中MaxOut方法和ReLU是目前常用的方法，坚决不要用sigmoid函数。可以用tanh，但是效果不会比上两种方法好。

ReLU方法：全称是Rectified Linear Unit，计算的是函数f(x)=max(0,x)的值，也就是说这个activation函数就是简单地以0为阈值，大于等于0的部分等于x，小于0的部分等于0。这个方法曾经在很长一段时间内很流行。

它相比sigmoid和tanh方法其收敛速度快得多；相比sigmoid和tanh类型，它在0点直接简单地设置了一个阈值界限，没有上述两个函数的指数运算。但LeRU也有它的缺点，

How BackPropagation Computes?

BackPropagation 是神经网络学习中通过recursive application来计算梯度的chain rule方法，这个算法或者叫做思想，对于有效地开发、涉及和调试Neural Networks具有非常重要的基石性作用。

1.【问题】：

BackPropagation要解决的问题，是在给定个函数f(x)和它的变量x的时候，计算f对于参数w，b的偏导数。而计算偏导数的目的是为了最终对w和b进行update迭代求参。

换而言之，BackPropagation的最终目的就是为了对w，b进行参数求解。

2.【chain rule的相关表达式】：

假设上述提到的f函数为：

1）x，y，z的初始值如下给出；

2）对f的表达式按照每个运算符号进行分层，设：q=x+y，f=q*z

那么根据给出的样本数据x,y,z

的值可以计算出q，f的值。这就是所谓的 forward pass 过程，计算每个运算步骤得到的值；

3）接下来是 backward pass 过程，这个过程的计算要从后面往前进行；

因为f=q*z，所以有：df/dz=q，df/dq=z；（即分别对q和z求偏导数）

同时，因为dq/dx=1，dq/dy=1，所以有：df/dx=df/dq*dq/dx*1.0 = z，和df/dy=df/dq8*dq/dy*1.0 = z；（这里的1.0是约定的最终表达式的对于自己本身的偏导数）

4）ok，到此，f对于x,y,z三个变量的偏导数都已经得到。具体如下代码。

上图中，绿色表示 forward pass过程计算得到的值，红色表示从后往前的backward pass过程计算得到的f对于各个计算模块的偏导数。

注：【circuit】表示上图中的直线连接起来的路径，可以理解为forward 和 backward 过程中的线路；圆圈中的运算符号通常被称为【gate】。

3.【Sigmoid example】

sigmoid 函数：

对这个函数中的参数求偏导比上面的例子要复杂很多，但是也无需担心，只需要跟之前的步骤一样按照运算符号进行逐级计算，就可以最终计算出偏导chain 结果。

开始计算之前需要知道以下这几个偏导数的计算公式：

于是，上面sigmoid 函数的forward 和backward 计算值如下图所示：

注：x0,x1 是明确给出的样本值；w0,w1,w2 是初始化的随机参数值，通常取接近于0的随机数值；

【forward pass】：上图中，forward计算很简单，已经给出了x值和w参数，只需要按照公司一步步计算即可；

【backward pass】：对于最后的红色初始偏导数值1.00，表示sigmoid 的f函数对于自己本身的偏导数值，可以想象为：f=f，可见偏导数当然为1.00；然后按照上上个图中的偏导公式，由此依次往前推导各个部分的偏导数，如-0.53其实是由df/dx=1/(-1)x^2=（-1）/(1.37)^2得来的。

---

结合上图中的公式和上上图中的链式推导结果，可以看出，sigmoid函数对于其变量的偏导数其实非常见到。上式可以当做一个常识记住哦。

更加详细的backward pass 推导过程参考下面的伪代码：

---

更加复杂的一个实践例子可以看下面这个：

---

【一些规律】：

1) 如上图所讲，对于+号构成的gate，其偏导数其实就等于+两边每个input的偏导数；
2) Max操作符，其偏导数等于input中较大的一个的偏导数，而较小的那个偏导数为0；
3) 而对于Multiply乘法gate，其一个input的偏导数等于gate的偏导数乘以另一个input的值；

小龟生病了

我的小乌龟生病了，白眼病，今天上网查了很多资料，希望可以把它治好。看着它们眼镜肿的鼓鼓的睁也睁不开，有点伤心着急了。

从网上查了一些关于白眼病的资料，去买了眼药水和药膏，回来给它们涂上。希望会慢慢好起来吧。

家里有个小动物，一下子增添了不少活气，唯一担心的就是它们的生老病死，实在让人痛心。

立

小时候老妈常对我说：三十而立。

三十而立这句话，古语就有云了呢，是说一个男人长大成人独当一面。

有时候回头想想，我的人生经历到现在，杂七杂八，什么都拼凑了一点，有好一点的，也有差一点的，虽然有点凌乱，但也还勉强算的上丰富。

作为一个比较念旧的人，我经常会在无聊的夜里想起以前的事情，会不时感慨时光飞逝的无情，也会在脑海里闪现过往里所有的开心和快乐，很小时候的事情，上小学的、中学的、高中的、大学的、研究生的，还有这四年工作的事情。我对于过去的回忆，更多的是对于彼时心境的怀念，也有一些对于成长历程的总结，但丝毫没有埋怨和记恨，我因此一直觉得很踏实，也很幸福。试想，如果有人能够再从我这里得到快乐，那该是非常美好的一件事情呢！看着别人幸福了，自己好像也就幸福了。

2014年，我走进了自己人生的第31个年头，现在的我两天不刮胡子就能堪比马克思恩格斯。

这几年，亲眼目睹了很多朋友走进婚姻，亲眼见证了很多幸福，虽然会有一点点觉得大家结婚后就不能跟曾经一样自由自在地相聚了，有那么一丝感伤，但看到一个个幸福，心中似乎也慢慢坦然，毕竟曾经只是过往，当下才是生活。我们彼此出现在生命里，彼此都是见证。

什么年龄就该干什么事！

今年，轮到我结婚了！

今天去试婚纱

今天跟老婆去试婚纱了，从来没有经验也没有听别人谈过，结果被坑得实在有点惨。一家住在青年汇102楼里的小商户，婚纱一上来就要了RMB 3980，礼服要了RMB 1580，不谈价，我们居然想都没细想就掏钱买了，也没有跟其他家比较，也没有上网查一下这个价钱是否合理。当时觉得还不错，样子挺好看，但是后来回家上网搜了一下，好看的太多了而且便宜。瞬间后悔了！

虽然说给老婆买东西尤其是婚纱不能太小气，但好歹也要注重性价比啊，毕竟又不是什么不差钱的大佬，还是要讲究一下的。

以后不能打肿脸充胖子了，这种话要勇敢地提醒老婆啊！我的钱也不是大风刮来的啊！ 5555~

              [ _ ]

姥姥（六）

2014年6月22日，姥姥的后事已基本料理完了，家里人把姥爷的后续生活也安排妥当，以后轮流在几个儿子女儿家里吃住，姥爷把家里的存款和东西大部分都分给了6个孩子，我有生以来第一次体会到了分家的感觉，挺不是滋味，尤其听妈妈说起舅舅们之间的那些个相互算计，唯恐怕吃了亏一样，我真的是打心眼里瞧不起这些没有意义的争斗，不是该一切为了老人麽，谁吃点亏占点便宜又能怎样。二姨的小家子气和唠叨无知也着实让我厌烦了，甚至开始同情二姨夫，我想，我以前是误会他了。

听老妈说，除了被分掉的东西，老房子的一切都会保持原样，修一修漏雨的房顶，姥姥衣柜里那些还很新的没怎么穿过的衣物基本该烧给她的都已忙完了，姥爷说，
“你姥姥老比衣裳了，都没拿么穿啊，布嘎希的，我说你留着干什么，等死了再穿？唉～”
姥姥和姥爷一生节俭，妈在收拾衣柜的时候翻出来很多很久以前的破衣服破布之类的，包括许艺凡刚出生的时候穿过的小裤子什么的。姥爷的一些鞋子，他都自己很仔细的用塑料袋包裹起来放在了柜子里，虽然有些土，但却看得出来做的时候很认真。

哥说，姥姥去世的那天晚上他做了一个梦，梦见姥姥的坟头开了好多花，很美。小姨也说做了一个梦，梦到有一只长得像凤凰的大鸟拍打着巨大的翅膀飞走了。也许，那是姥姥的化身吧，我想。

其实，姥姥已经走了，我最担心的是姥爷，不担心他吃不饱穿不暖，担心他在舅舅家受几个舅妈的气。老妈说，她会每隔几天就回去看望他。在老妈这个女汉子强力的监督下，相信不会。

妈说，姥姥的葬礼收到了75个包袱，昨天去带孝的人也很多，可怜姥姥生前的威望，听姥爷说以前这方圆几公里内的村子，谁家的红事白事基本都是姥姥给操办的。妈说，姥姥生前积了太多公德。

姥姥（五）

2014年6月20日凌晨0点30分，我到家了，老爸出门迎我。停好车进屋，老爸说老妈给他打了好几个电话说我晚上到家，说我可能没吃饭，让他给我做点面条，她要在姥姥家彻夜守灵。

一进家门，听老爸声音声音好像不对，我问他，
“爸，你是为我姥姥哭了？还是怎么了？声音不太对。”
“没，我啊，这两天有点感冒。”

我就着腊肠吃了两碗面条，吃完已是凌晨1点半左右，接着跟老爸在东炕上躺下了，聊了好一会姥姥的事情，一直到2点多老爸说，
“睡吧，明天早上还要早起，7点你姥姥就要去火化了。”
“恩，好。”

这一夜，我却怎么也睡不着，明明已经很困了。不知过了多久，我被老爸起床的声音吵醒，我睁开双眼，天才微微亮，才4点多。于是，我也再睡不着了，上一下厕所，在院子里走一走。

吃过早饭，还是面条就着灌肠。我开车带老爸一起过去。一进姥姥家门，先映入眼帘的不再是姥姥和姥爷走出院门来迎我的笑脸，而是那许多身穿白色孝服的人，妈和小姨他们都在屋里坐着守灵。

我一脚踩在灵前的麻袋上，突然觉得两条腿好软，一下子跪在了地上，眼泪，哗地出来了，我最爱的姥姥再也回不来了，灵前播放着她生前经常听的菩提音带，我总觉得她就坐在炕上听，上次回家的时候还好好的，叫我怎么愿意相信。好好的一个人，怎么说没就没了呢？