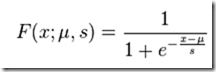Logistic Regression

Logistic Regression is a classical Classification method. It is the same with Maximum Entropy Model as Log linear Model.

（还是用中文说吧，用英文太扭捏了。）

首先提一下Logistic Distribution，即逻辑斯蒂分布，其在数学上的定义和公式如下：

定义（逻辑斯蒂分布）设X是连续随机变量，X服从逻辑斯蒂分布是指X具有下列分布函数和密度函数：

公式中，u为位置参数，r>0为形状参数。分布函数和密度函数的曲线图像如下：

从曲线图示可以看出，逻辑斯蒂分布函数是一个S形曲线，曲线在中心附近增长较快，在两端增长速度较慢。

【注】将Logistic Regression 应用到二分类中的话，可以将S形曲线的上半段和下半段分别看作是二分类的两类区间，如果待分类数据的Logistic Regression值落在了某一段则其就分类到某一类中，并且Logistic Regression的概率值离中心点u越远，则分到该类的可能性越大。

定义（逻辑斯蒂回归模型）：二项Logistic Regression回归模型是如下的条件概率分布：

P（Y=1|X） = exp（w·x + b）/（1+exp（w·x + b））

P（Y=0|X） = 1/（1+exp（w·x + b））

这里，X属于n维R实数域向量表示输入，Y属于{0,1}表示输出的类标签，w也属于n维R实数域表示Logistic Regression模型的参数集合，b也是参数。w称为权值向量，b称为偏置。w·x表示w和x的内积。

 

（二分类）：

在使用Logistic Regression 进行二分类时，根据上面的回归模型的公式，我们根据训练语料可以得到输入X，输出Y，因此要训练得到回归模型就是要学习得到参数w和b，一旦知道了符合训练语料的最优参数w和b，之后再随机给出一个输入X，在w和b已知的条件下就可以计算出X对应的最优Y分类是0还是1，并且可以给出具体的概率来衡量。

模型参数估计：采用极大似然估计来计算模型参数，学习过程通常采用 梯度下降法 或者 拟牛顿法。

因为是二分类，设：

P（Y=1|X）=pi（x）

P（Y=0|X）=1 – pi（x）

那么似然函数，即在训练语料上作分类后每一条数据的分类所得概率之乘积为：

A =

A 的值越大，表明分类越准确，也就是模型越优。

从而，要求最优参数w和b使得似然函数A 的值最大即可，即求A的极大值。

取log后得：

L（w）=

=

=

=

对L(w)求极大值，得到w的估计值，即模型参数。有了模型参数就有了模型。

 

（多分类）：

以上为logistic regression模型在二分类上的应用，可以推广到多分类的情况。在二分类的情况下，参数w为在1和0两类上分别对应一个n维参数向量（w1,w2，，，，wn），在多分类情况下则在每一类上都对应一个n维参数向量。在实际编码过程中可将w存放在一个n*m维的矩阵，其中n为类数目，m为最大特征数。

多分类情况下的logistic regression公式为：

P（Y=k|X）=

跟二项logistic regression的似然函数类似，多项的似然函数为：

L(w) =

在所有N条训练数据上进行分类，分类结果在正确类别上的概率进行乘积运算，最终得到L（w），当参数w使得L（w）的值最大时，w即为最终模型。

对L（w）求极大值，得到参数矩阵。具体可采用梯度下降法或者拟牛顿法。